Notasi Sigma dan Induksi Matematika: Rumus, Contoh Soal

A. Notasi Sigma

Sigma dalam bahasa sederhananya dapat dikatakan sebagai jumlah. Notasi sigma adalah simbol untuk menjumlahkan sejumlah bilangan terurut yang mengikuti suatu pola dan aturan tertentu. Materi notasi sigma masih mempunyai hubungan dengan materi barisan dan deret, baik aritmetika atau geometri. Secara umum, notasi sigma diberikan pada persamaan di bawah.

Suatu deret 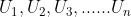$U_{1}, U_{2},U_{3},......U_{n}$ jika dijumlahkan seluruhnya menjadi : 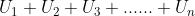$U_{1}+ U_{2}+ U_{3}+......+U_{n}$ dapat ditulis sebagai berikut.

$\sum_{i=1}^{n}U_{i}$

Bentuk

$\sum_{i=1}^{n}U_{i}$ dengan tujuan untuk melakukan penjumlahan suku-suku $U_{i}$ dalam barisan $\left [U_{i}\right ]$ , mulai dari i = 1 sampai dengan i = n.

Aturan Notasi Sigma

Aturan aljabar notasi sigma berdasarkan bukti pada sifat-sifat bilangan real sebagai berikut:

$\therefore \sum_{i=1}^{n} U_{i}=\sum_{j=1}^{n}U_{j}$

$\therefore \sum_{i=1}^{n} c\, = c\, n,\, c=\, konstanta$

$\therefore \sum_{i=1}^{n}c\, U_{i}=c\, \sum_{i=1}^{n}U_{i},\, \, c=konstanta$

$\therefore \sum_{i=1}^{n}(U_{i}\pm V_{i})\, =\, \sum_{i=1}^{n}U_{i}\pm \sum_{i=1}^{n}V_{i},\, \, c=konstanta$

$\therefore \sum_{i=1}^{n}(U_{i}\pm V_{i})^{2}\, =\, \sum_{i=1}^{n}U_{i}^{2}\pm 2\sum_{i=1}^{n}U_{i}V_{i}\pm \sum_{i=1}^{n}V_{i}^{2},\, \,$

$\therefore \sum_{i=1}^{c}\, U_{i}\, +\,\sum_{i=\, c+1}^{n}\, U_{i}\,=\, \sum_{i=1}^{n}U_{i}\,$

$\therefore \sum_{i=1}^{n}\, U_{i}\, =\sum_{i=1-k}^{n-k}\, U_{i+p}= \sum_{i=1+p}^{n+p}\, U_{i-p}$

$\therefore \sum_{i=k}^{m}\, U_{i}\, =\sum_{i=1}^{m-k+1}\, U_{i+k-1}$

Untuk memahami permasalahan tentang Notasi sigma beserta aturan/sifat-sifatnya , perhatikan contoh soal dan pembahasan soal berikut:

Contoh 1:

Ubahlah

$\sum_{k=0}^{5}\, (4k+3))\,$ menjadi bentuk sigma dengan bawah 5 !

Pembahasan:

$\sum_{k=0}^{5}\, (4k+3))\,=\sum_{k=5}^{5+5}4(k-5)+3=\sum_{k=5}^{10}4k-20+3=\sum_{k=5}^{10}4k-17$

Contoh 2:

Nilai dari

$\sum_{i=1}^{6}\, (4i+3))\,=.....$

$\sum_{i=1}^{6}\, (4i+3))\,=(4.1+3)+(4.2+3)+(4.3+3)+(4.4+3)+(4.5+3)+(4.6+3)$

$\sum_{i=1}^{6}\, (4i+3))\,=7+11+15+19+23+27=102$

Contoh 3:

$Nilai \, dari\, \sum_{k=1}^{4}(k^{2}+2k)=.....$

Pembahasan:

$\sum_{k=1}^{4}(k^{2}+k)=(1^{2}+1)+(2^{2}+2)+(3^{2}+3)+(4^{2}+4)$

$\sum_{k=1}^{4}(k^{2}+k)=(1^{2}+1)+(2^{2}+2)+(3^{2}+3)+(4^{2}+4)=2+6+12+20=40$

Contoh 4:

$Bentuk \, \, notasi\, sigma \, \, 3+8+13+.....+73\, \, adalah.....$

$A.\sum_{k=1}^{15}(5k-2)$

$B.\sum_{k=3}^{73}(k-2)$

$C.\sum_{k=3}^{73} 5k$

$D.\sum_{k=1}^{15} (5k-3)$

$E.\sum_{k=2}^{15} (2k-2)$

Pembahasan:

Dari soal tersebut diperoleh bahwa suku pertama atau a = 3 dan selisih dua buah suku berurutan atau beda (b) adalah 5, maka diperoleh bahwa deret tersebut adalah deret aritmatika. Sehingga dapat dirumuskan dengan:

$S_{n}=\frac{n}{2}(2a+(n-1)b)$

Untuk menentukan banyaknya n dapat ditentukan dengan cara:

$U_{n}=a + (n-1)b$

$73=3+(n-1)5$

$70=5(n-1)$

$14=n-1$

$n=15$

maka dapat ditulis dalam notasi sigma:

$\sum_{k=1}^{15}(5k-2)$

Contoh 5:

$Diketahui\, \, \sum_{i=6}^{25}P_{i}=10. \, Nilai\,\sum_{i=6}^{25}(2+P_{i})=....$

A. 50

B. 60

C. 70

D. 80

E. 90

Pembahasan:

$\sum_{i=6}^{25}(2+P_{i})=\sum_{i=6}^{25}2+\sum_{i=6}^{25}P_{i}$

$\sum_{i=6}^{25}(2+P_{i})=\sum_{i=6-5}^{25-5}2+\sum_{i=6}^{25}P_{i}= \sum_{i=6-5}^{25-5}2+\sum_{i=6}^{25}P_{i}$ $\sum_{i=6}^{25}(2+P_{i})=\sum_{i=1}^{20}2+\sum_{i=6}^{25}P_{i}= 2.20\, +\, 10=50$

Contoh 6:

$Nilai\, \sum_{n=2}^{21}(5n-6)=....$

A. 882

B. 1030

C. 1040

D.1957

E. 2060

Pembahasan:

$Dari\, \, notasi\, sigma\, \, \sum_{n=2}^{21}(5n-6)\, diperoleh:$

$\sum_{n=2}^{21}(5n-6)\, =\left ( 5.2-6 \right )+\left ( 5.3-6 \right )+\left ( 5.4-6 \right )+\left ( 5.5-6 \right )....(5.21-6)$

$\sum_{n=2}^{21}(5n-6)\, =4+9+14+19+........+99$

maka diperoleh: a = 4

b = 9-4 = 5

n = n(akhir) -(n(awal)-1) = 21 - (2-1) = 20

maka untuk menentukan

$\sum_{n=2}^{21}(5n-6)\,$

yaitu dengan rumus deret aritmatika sebagai berikut:

$S_{n}=\frac{n}{2}\left ( a+U_{n} \right )$

Maka:

$S_{n}=\frac{20}{2}\left ( 4+99 \right )=10.\left ( 103 \right )=1030$

Contoh 7:

$Diketahui\, \, \sum_{k=5}^{25}\left (2-pk \right )=0,\, \, maka \, nilai\,\sum_{k=5}^{25} pk=....$

A.20

B.28

C.30

D.42

E.112

Pembahasan:

$\sum_{k=5}^{25}\left (p-2k \right )=0,$

$\sum_{k=5}^{25}\left (p-2k \right )= \sum_{k=5}^{25}p-\sum_{k=5}^{25}2k=0$

$\sum_{k=5}^{25}\sum_{k=5}^{25}2k$

$2(n(akhir)-(n(awal)-1)=\sum_{k=5}^{25}pk$

$2(25-(5-1))=\sum_{k=5}^{25}pk$

$maka\, :\sum_{k=5}^{25}pk=42$

Demikian materi dan contoh notasi sigma,semoga bisa dipahami dengan baik. Sekarang kita bahas materi berikutnya yaitu Induksi Matematika.

B. Induksi Matematika (Aksioma Peano)

Salah satu aksioma Peano menyatakan jika suatu pernyataan benar untuk $n=1$ dan jika kebenaran pernyataan itu untuk $n=k$ mengakibatkan kebenaran pernyataan untuk $n=k+1,$ maka pernyataan itu benar untuk setiap bilangan asli $n.$

Prinsip Dasar Induksi Matematika:

Ada tiga langkah dalam induksi matematika yang dibutuhkan untuk membuktikan suatu rumus ataupun pernyataan. yaitu :

Pembuktian pada rumus ataupun pernyataan P(n), dimana tergantung sesuatu "benar" untuk n = 1
Pembuktian pada rumus ataupun pernyataan P(n), dimana tergantung sesuatu "benar" untuk n = k
Terakhir adalah membuktikan pada rumus ataupun pernyataan P(n), dimana tergantung sesuatu "benar" untuk n = k + 1

Prinsip diatas dapat diperluas untuk pernyataan yang bergantung pada himpunan bagian tak kosong dari bilangan asli yaitu:

============================================================================================================================================================

Misalkan P(x) adalah suatu pernyataan dan P(x) benar untuk setiap bilangan asli x ≥ y jika memenuhi 2 hal berikut :

P(y) benar, artinya untuk x = y, maka P(x) bernilai benar
Untuk setiap bilangan asli z ≥ y, jika P(z) benar maka P(z + 1) juga benar.

Untuk memahami permasalahan tentang Induksi Matematika, perhatikan contoh soal dan pembahasan soal berikut:

Contoh 1:

$Buktikan\, bahwa \, \, 1+3+5+7+.....+(2n-1)=n^{2}, untuk\, setiap\, bilangan\, asli\, n!$

Pembahasan:

Langkah 1:

Membuktikan bahwa pada rumus ataupun pernyataan P(n), "benar" untuk n = 1

$P(n)=n^{2},\, dan\: untuk\: n=1\: maka\: P(1)=1^{2}=1\: terbukti \: benar$

Langkah 2:

Membuktikan bahwa pada rumus ataupun pernyataan P(n), "benar" untuk n = k

$P(n)=n^{2},\, dan\: untuk\: n=k\: maka \:diasumsikan\: P(k)=k^{2}\: \:adalah\: benar$

Langkah 3:

Membuktikan bahwa pada rumus ataupun pernyataan P(n), "benar" untuk

Contoh 2:

$Buktikan\: untuk \, semua \, bilangan \, bulat \, tidak \, negatif \, n \, berlaku \, bahwa\, 2^{0}+2^{1}+2^{2}+2^{3}+......+2^{n}=2^{n+1}-1$

Pembahasan:

Langkah 1:
Membuktikan bahwa pada rumus ataupun pernyataan P(n), "benar" untuk n = 0

$2^{0}+2^{1}+2^{2}+2^{3}+.....+2^{n}=2^{n+1}-1$

Untuk n = 0 diperoleh:

$P(n)=2^{n+1}-1$

Langkah 2:

Membuktikan bahwa pada rumus ataupun pernyataan P(n), "benar"

untuk n = k

$2^{0}+2^{1}+2^{2}+2^{3}+....+2^{k} \: =2^{n+1}-1 \:=2^{k+1}-1=2.2^{k}-1$

Langkah 3:

Membuktikan bahwa pada rumus ataupun pernyataan P(n), "benar" untuk n = k+1

$2^{0}+2^{1}+2^{2}+2^{3}+.......+2^{k}+2^{k+1}=2^{(k+1)+1}-1 \:\,$

$Jika \: \, diasmumsikan \:\, bahwa \: \, 2^{0}+2^{1}+2^{2}+2^{3}+.......+2^{k}=2^{k+1}-1 \:\, adalah \:\, benar$

$maka\, \, 2^{0}+2^{1}+2^{2}+2^{3}+.......+2^{k}+2^{k+1}=2^{(k+1)}-1+2^{k+1}$

$2^{0}+2^{1}+2^{2}+2^{3}+.......+2^{k}+2^{k+1}=2.2^{(k+1)}-1$

$2^{0}+2^{1}+2^{2}+2^{3}+.......+2^{k}+2^{k+1}=2^{(k+1+1)}-1$

$2^{0}+2^{1}+2^{2}+2^{3}+.......+2^{k}+2^{k+1}=2^{(k+1)+1)}-1$

$Terbukti\, \, bahwa\, \, 2^{0}+2^{1}+2^{2}+2^{3}+.......+2^{k}+2^{k+1}=2^{(k+1)+1)}-1$

Contoh 3:

$Buktikan\, \, bahwa \, \, untuk \, \, setiap \, \, n\geqslant 0,maka\, \, 2^{3n}-1 \, \, habis \, \, dibagi\, \, 7$

Penyelesaian:

Langkah 1:

$Perhatikan \, \, bahwa \, \, untuk \, \, n=0:\, P(n)=2^{3.0}-1=1-1 \, \, habis \, \, dibagi\, \, 7$

Langkah 2:

$Asumsikan \, \, bahwa \, \, P(k) \, \, benar \, \, untuk \, \, suatu \, \, k\geqslant 0. \, \, Oleh \, \, karena \, \, itu, \, \, untuk \, \, suatu \, \, \, \, k\geq 0 \, \, berlaku\, \, 2^{3k}-1 \, \, adalah\, \, kelipatan \, \, 7. \, \, Artinya \, \, terdapat \, \, bilangan \, \, bulat \, \, p \, \, sedemikian \, \, sehingga \, \, 2^{3k-1}=7p$

Langkah 3:

$Selanjutnya \, \, akan \, \, ditunjukkan \, \, kebenaran \, \, dari \, \, pernyataaan \, \, P(k+1), \, \, artinya \, \, akan \, \, dibuktikan \, \, 2^{3(k+1)}-1\, \, kelipatan \, \, 7 \, \, (terdapat \, \, bilangan \, \, bulat \, \, sedemikian \, \, sehingga \, \, 2^{3(k+1)}-1=7q)$

$2^{3(k+1)}-1=2^{3k+3}-1$

$2^{3(k+1)}-1=2^{3}.2^{3k}-1$

$2^{3(k+1)}-1=8.2^{3k}-8+7$

$2^{3(k+1)}-1=8(2^{3k}-1)+7b$

$2^{3(k+1)}-1=8.7p+7$

$2^{3(k+1)}-1=7(8p+1)=7q$

$Dari\, \, penjelasan \, \, di \, \, atas \, \, terbukti \, \, bahwa \, \, P(k+1)\, \, benar , \, \, sehingga terbukti \, \, P(n) \, \, benar \, \, untuk \, \, setiap \, \, n\geq 0$ Contoh 4:

$Buktikan \, \, bahwa\, \, 1 + 2 + 3 + \, \,.... + n = \frac{1}{2}\, n(n+1) \, \, untuk \, \, setiap \, \, n \, \, bilangan \, \, integer \, \, positif \, \, adalah. . .$

Pembahasan:

Langkah 1:

$Dari\, \, 1 + 2 + 3 +....+ k = \frac{1}{2}.n (n+1) \, \,$

$Untuk \, \, n = 1 \, \, akan \, \, diperoleh\, \, :$

$1 = \frac{1}{2}\, .1 . (1+1) \rightarrow 1 = 1 \, \, (benar)$

Langkah 2:

$misalkan\, \, untuk \, \, n = k \, \,, diasumsikan\, \, 1 + 2 + 3 +....+ k = \frac{1}{2}.k (k+1) \, \, adalah \, \, benar$

Langkah 3:

$Untuk \, \, n = \, \, k+1 \, \, berlaku\, \, 1 + 2 + 3 +...+ (k+1) = \frac{1}{2}(k+1) (k+2)$

$Karena\, \, 1 + 2 + 3 +...+ k = \frac{1}{2}(k) (k+1)$

maka:

$\, 1 + 2 + 3 +...+ k+k+1 = \frac{1}{2}(k) (k+1)+(k+1)$

$\, 1 + 2 + 3 +...+ k+k+1 = \left ( k+1 \right )\left ( \frac{1}{2}k+1 \right )$

$\, 1 + 2 + 3 +...+ k+k+1 = \left ( k+1 \right )\left ( \frac{k+2}{2} \right )$

$\, 1 + 2 + 3 +...+ k+k+1 = \frac{1}{2}\left ( k+1 \right )\left ( k+2 \right )$

Dari penjelasan diatas terbukti bahwa:

$\, 1 + 2 + 3 +...+ n = \frac{1}{2}\left ( n \right )\left (n+1 \right ) untuk \, \, setiap \, \, n \, \, bilangan \, \, integer \, \, positif$

Contoh 5:

$Buktikan \, \, bahwa\, \, n^{3}+ 2n\, \, adalah \, \, kelipatan \, \, 3 \, \, untuk \, \, setiap \, \, n \, \, bilangan\, \, bulat\, \, positif\, \, adalah. . .$

Pembahasan:

Langkah 1;

$Jika\, \, P(n)=n^{3}+ 2n\, \, adalah \, \, kelipatan \, \, 3 \, \,maka:$

$Untuk\, \, n=1 \, \, maka: P(1)=1^{3}+ 2(1)=3\rightarrow adalah \, \, kelipatan\, \, 3\, \, (benar)$

Langkah 2:

$misalkan \, \, untuk \, \, n = k, asumsikan k^{3}+ 2k = 3p\, \, benar$

langkah 3:

$Untuk\, \, n = k + 1\, \, berlaku \, \, (k+1)^{3} + 2(k + 1) \, \, adalah \, \, kelipatan \, \, 3$

$Dengan \, \, menggunakan \, \, binomial\, \, Newton:(k + 1)^{3}=k^{3}+3k^{2}+3k+1,\, \,$

Sehingga:

$(k + 1)^{3}+2(k+1)=k^{3}+3k^{2}+3k+1+2k+2$

$(k+1)^{3}+2(k+1)=\left ( k^{3}+2k \right )+3(k^{2}+k+1)$

$Karena: k^{3}+2k\, \, =3p\rightarrow kelipatan\, \, 3,maka:$

$(k+1)^{3}+2(k+1)=3p+3(k^{2}+k+1)$

$(k+1)^{3}+2(k+1)=3(p+k^{2}+k+1)$

$Jika\, \, (p+k^{2}+k+1)\, \,=m,\, \, maka\, \, diperoleh \, \, 3(p+k^{2}+k+1)=3m\, \, adalah\, \, kelipatan \, \, 3,$

Dari penjelasan di atas, terbukti bahwa:

$n^{3} + 2n \, \, adalah \, \, kelipatan\, \, 3 \, \, untuk \, \, setiap\, \, n\, \, bilangan\, \, bulat\, \, positif$

Contoh 6:

$Buktikan \, \, bahwa \, \, 2^{n} > n + 20, \, \, untuk \, \, setiap \, \, bilangan \, \, bulat \, \, n \geq 5\, \, adalah. . ..$

Pembahasan:

Langkah 1:

$Misalkan\, \, P(n)= 2^{n} > n + 20, sehingga:$

$Untuk\, \, n=5\, \, maka:\, \, P(5)= 2^{5} > 5 + 20\rightarrow 32> 25\, \, (benar)$

Langkah 2:

$Untuk\, \, n=k\, \, maka:\, \, asumsikan \, \, P(k)= 2^{k} > k + 20,benar,sehingga:$

Langkah 3:

$Akan \, \, dibuktikan\, \, untuk\, \, n=k+1\, \, maka:\, \, P(k+1)= 2^{k+1} > (k+1) + 20,benar,sehingga:$

$2^{k+1} > 2^{k}.2$

$Karena\, \, 2^{k}>k+20,\, \, maka:2^{k+1} > 2^{k}.2>2(k+20)$

$2^{k+1} > 2^{k}.2>2(k+20)=2k+40> (k+1)+20,\, \, untuk\, \, setiap\, \, k\geq 5$

Dar penjelasan di atas,maka terbukti bahwa:

$2^{n} > n+20 \, \, untuk\, \, setiap\, \, k\geq 5$